Spherical Textures
There are many ways to apply a texture map to a sphere. It is an
important process because of applications such as texture-mapping the entire
surface of the earth.
- naive approach: directly map latitude-longitude onto sphere
- source: a single rectangular texture with a proportion of 2x1
- texture coordinates: u goes from 0 to 1 around the equator, v goes from 0 to
1 from pole to pole
- pro: simple, most data sources are already in this format
- con: wastes the majority of the texture resolution at the poles,
where it is usually least needed
-
BlueMarbleViewer
used this approach, as did apparently a few other early spinny globes
- cubic mapping
- source: 6 textures corresponding to sides of a cube surrounding the
sphere
- uv mapping is projected (e.g. with
Gnomonic
Projection) from the surface of the sphere to the sides of the cube
- pro: more evenly distribution of texels than the naive approach
- con:
- the projection is a non-linear warp, making the computation
difficult
- still has wide variation in ratio of texels/surface area
- For many other possibilities, see
Map Projections: Cubic Globes
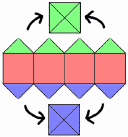 Omnitect mapping
Omnitect mapping
- like cubic mapping, uses four equatorial textures and two polar
- however, the equatorial textures use a direct lat-lon mapping, and
the poles are treated specially by joining four spherical right
triangles of the top and bottom latitudes
- pro: takes advantage of simple direct lat-lon mapping for most of
the non-polar surface
- con
- complicated special cases for the tile boundaries
- two types of mapping with different requirements for subdivision
and projection
- detail: see slides on
global
tiling system
- icosahedral mapping

- like cubic mapping, but using an icosahedron
- source: pairs of the icosahedron's faces can be joined into quads,
for 10 square source textures
- uv mapping: uv is simply (0,0), (1,0), (0,1) at the corners of each
triangular face
- pro:
- less distortion than other approaches, evenly distributed
texels/surface area
- elegant system of identical regular triangles
- con:
- rendering must explicitly store and draw all 20 faces of the
icosahedron
- more tile boundaries to deal with
- when applied to the earth with boundaries arranged to avoid breaking
land masses, this is known as Buckminster Fuller's Dymaxion Projection
-
 another
icosahedral system is the
Pyxis Digital Earth Reference Model (DERM)
another
icosahedral system is the
Pyxis Digital Earth Reference Model (DERM)
- they call it a "Icosahedron Snyder Equal Area Aperture 3 Hexagonal Grid"
(ISEA3H)
- this provides a way to index every point on the earth, without
using lat-lon or any conventional coordinate system
- octahedral
-
Aasgaard's
map projection
-
 developed for the Norkart
Virtual Globe, Rune Aasgaard's
map projection page has a good PowerPoint presentation illustrating
the approach, example source code of the transformation, and other
supporting documents
developed for the Norkart
Virtual Globe, Rune Aasgaard's
map projection page has a good PowerPoint presentation illustrating
the approach, example source code of the transformation, and other
supporting documents
- basically maps a quadtree onto a Mercator-like projection, with the
depth of the tree's branches decreasing towards the poles
- benefit is that the texels stay close to square
- disadvantage is that the poles behave badly (distortion, wasted
texture memory) which is often not a problem since they are "small and
usually insignificant"
- published academically as "Projecting a Regular Grid onto a
Sphere or Ellipsoid", Rune Aasgaard, in: "Advances in Spatial
Data Handling", Dianne Richardson and Peter van Oosterom (eds.),
Springer-Verlag 2002, pp 339-350
- ORBITER Space Flight Simulator
- free (but closed-source), supports paging of a ~2km
earth texture (16kx8k)
- the author, Martin Schweiger explains: "Orbiter
splits the surface into latitude strips, and each latitude strip is cut
into n patches, where n is approximately proportional to cos(latitude),
to maintain a roughly constant resolution level at all latitudes.
Orbiter also uses a multi-resolution approach, where the patch size and
resolution is dependent on the apparent diameter of the planet and
camera distance from the surface. It also
implements a culling mechanism which renders only patches that are
visible from the camera position (so that the render load is roughly
independent of camera altitude and texture resolution), and it allows
the application of spatially varying surface texture resolutions (e.g.
higher resolution around interesting features."
Resources

 Omnitect mapping
Omnitect mapping
 another
icosahedral system is the
Pyxis Digital Earth Reference Model (DERM)
another
icosahedral system is the
Pyxis Digital Earth Reference Model (DERM) developed for the Norkart
Virtual Globe, Rune Aasgaard's
map projection page has a good PowerPoint presentation illustrating
the approach, example source code of the transformation, and other
supporting documents
developed for the Norkart
Virtual Globe, Rune Aasgaard's
map projection page has a good PowerPoint presentation illustrating
the approach, example source code of the transformation, and other
supporting documents